原文地址：http://cs231n.github.io/linear-classify/
翻译：Archiew 　转载需注明出处

线性分类

目录
引入线性分类
线性得分函数
解释线性分类器
损失函数
　多类SVM
　Softmax分类器
　SVM与Softmax
线性分类器Web交互式演示
总结

线性分类

上一讲中，我们介绍了图像分类的问题，即从一组固定的类别中为图像分配单个标签的任务。更重要的是，我们描述了k-最近邻（kNN）分类器，它通过将图像与训练集中的（带注释的）图像进行比较来标记图像。正如我们所看到的，kNN有许多缺点：

• 分类器需要存储所有训练数据以供接下来与测试数据作比较。因为数据集大小很容易达到千兆字节，所以这会导致空间效率低下。
• 对测试图像的分类很耗费资源因为它需要与训练集中的所有图像进行比较。

预览 接下来我们要开发出来一种更加高效的方法去进行图像分类，最终自然地扩展到整个神经网络和卷积神经网络。该方法涉及两个主要部分：将原始数据映射为分类得分的score function(得分函数)，量化预测分数和真值标签之间差异的lose function(损失函数)。我们将这个问题看作优化问题：最小化关于得分函数参数的损失函数。

线性得分函数

首先定义得分函数，该函数将图像像素值映射为每个分类的置信度分数。接下来通过一个具体例子来说明。假定图像训练集\(x_i\in{R^D}\)，与之对应的标签集为\(y_i\)，其中\(i=1…N\),\(y_i\in{1…K}\)。也就是说，我们有\(N\)个样本(每个样本维度\(D\))和\(K\)个独立标签分类。例如，对于CIFAR-10，我们的训练集有\(N=50,000\)个图片，每个图片有\(D=32X32X3=3072\)个像素，独立分类数\(K=10\)。我们现在定义原始像素映射到分类得分的得分函数：$$f:R^D→R^K$$
线性分类器(Linear classifier) 在这里，我们从最简单的线性映射开始：$$f(x_i,W,b)=Wx_i+b$$在上述等式中，假定图片\(x_i\)已经被平铺成一个单一列向量[Dx1]。矩阵\(W\)(大小：[KxD])和向量\(b\)(大小：[Kx1])是函数的参数。在CIFAR-10中，\(x_i\)是第i个被平铺成[3072x1]的图片，\(W\)是[10x3072],\(b\)是[10x1]，也就是我们输入3072个像素值，并获得代表分类得分的10个数据输出。参数\(W\)被称作权重，\(b\)被称作偏差向量因为它影响输出得分但并不与真实数据\(x_i\)交互。
注意：

• 单一矩阵相乘\(Wx_i\)有效地并行评估10个独立分类器，\(W\)中的每行都是一个分类器
• 输入数据\((x_i,y_i)\)是给定的，我们控制参数\(W,b\)的设置。目标是计算全部训练集中图片分类得分并与真值分类标签相匹配。直观上我们希望正确分类能够得到比错误分类更高的分数
• 这种方法的一个优势是训练集用来学习参数\(W,b\)，一旦学习完成，就可以完全抛弃训练集只保留学习到的参数。因为新的测试图片可以通过此函数进行简单的前向传递并且基于得分进行分类
• 最后，注意到对测试图片的分类仅涉及到一次矩阵乘法和加法，这将比之前的比较测试图片与训练图片差异快得多。

卷积神经网络将图像像素映射为上述提到的得分，但是映射\(f\)将会更复杂并且包含更多的参数

解释线性分类器

注意到线性分类器计算图像3个通道所有像素值的加权和作为分类得分。根据我们设置的权重值的精度，映射函数能够反映出对图片某些位置某种颜色的倾向。例如，设想图像中有许多蓝色像素点(可能被看作是‘水’)可能被分类为‘船’。我们可能希望‘船’分类器在图片蓝色通道上有许多正权重值(蓝色的存在会增加船分类的得分)，而在红/蓝通道上有负权重值(红/蓝的存在会降低船分类的得分)。

将图像类比为高维点 因为图片被平铺为高维列向量，因此我们可以将图片对应到高维空间内的一个点(eg.CIFAR-10中的每个图片都可对应为3072维空间中的一个点)。类似地，整个数据集就对应该空间中的一组(含标签)点集。
因为我们定义分类得分为图像像素加权和，所以每个分类得分是整个空间的线性函数。我们无法可视化3072维空间但是设想将其压缩为2维，然后尝试可视化分类器的操作过程。

\(W\)中的每行对应一个分类的分类器。这些数的几何解释是，当我们改变\(W\)的每一行，像素空间对应线将会旋转不同方向。另一方面偏差\(b\)允许我们的分类器翻转这条线？？？尤其要注意的是没有偏差的话，对输入\(x_i=0\)将会输出0分，无论权重值为多少，因此所有线将会穿过原点。（这段没太懂）

将线性分类器解释为模板匹配 权重\(W\)的另一种解释是每行对应一个分类模板(或者称作‘原型’)。对一个图片，每个分类的得分是通过比较每个模板和图片的内积(或点积)获得。用专业术语说，线性分类器在做模板匹配，而模板是在不断学习的。其实我们还是在做最近邻工作，只不过这里使用内积来代替L1或L2距离。

除此之外，注意到上图中马的模板似乎包含了一个‘双头’马，这是因为数据集中包含了面向左侧和面向右侧两种含马的训练图片，线性分类器将这两个模型合并到一个模板图中。类似地，汽车模板似乎合并了多个模型(不同角度不同颜色)到一个模板中。最终的模板呈现红色，表明数据集中含有大量红色汽车图片。那么实际上这个线性分类器在正确识别不同颜色汽车方面还有所欠缺，随后我们在神经网络中会做这部分工作。神经网能够通过隐藏层中的中间神经元来检测特殊的汽车类型(eg.向左的绿色汽车，向前的蓝色汽车)，后层神经元可以将这些结合起来得到更精确的汽车分类得分。
偏差技巧 为简化，这里有个小技巧，我们可以将参数\(W,b\)合为一个。常用方法是将两个参数集结合成一个单一矩阵，具体要通过扩展向量\(x_i\)的维度(增加一列)，多余出来的量默认用1来填充。这样，之前的得分函数就会变成下面这样单一矩阵乘法：$$f(x_i,W)=Wx_i$$还以CIFAR-10为例，\(x_i\)将由[3072x1]变为[3073x1]，\(W\)由[10x072]变为[10x3073]。\(W\)中多出来的列对应于偏差\(b_i\)。下面的图可能会便于理解：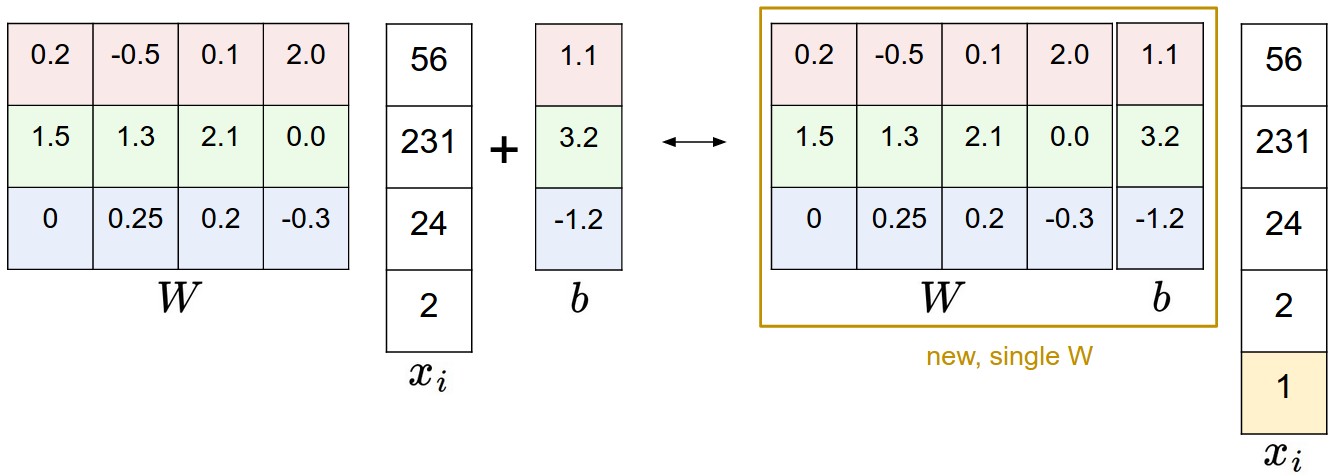

图片预处理 上面例子中我们使用图像原始像素([0…255])，在机器学习中，更为常见的是规范化我们的输入。尤其重要的是通过减去每个特征的均值来中心化数据。对于图像而言就是要计算训练图片的均值，然后用每个图像去减去它得到像素范围在[-127,127]的图像。更进一步的常用方法是将每个图像像素值缩放至[-1,1]。零均值中心可能更重要，但我们打算放到理解了梯度下降之后再来讲。

损失函数

上面章节定义了从像素值到分类得分的映射函数，通过一系列权重\(W\)使其参数化。我们希望通过调整权重值来达到预测分类得分和训练数据分类标签结果一致。
上面对猫的图片分类中，由于我们提供了随意的权重值，导致猫的分类得分远小于其他两个分类得分。我们将用一个损失函数(或叫成本函数，目标)来衡量得分结果与图片分类真值的差异。直观来讲，好的分类结果对应低的损失值，与之对应，坏的分类结果对应高的损失值。

　多类SVM损失

定义损失函数细节的方法有多种，我们先以常用的损失函数多类支持向量机(SVM)损失为例。通过固定余量Δ设置SVM损失使得SVM对于正确分类有较高的得分(相对于错误分类得分)。值得注意的是，正如我们上面所做的那样，有时候对拟人损失函数有所帮助：SVM希望在某种程度上产生更低的损失。
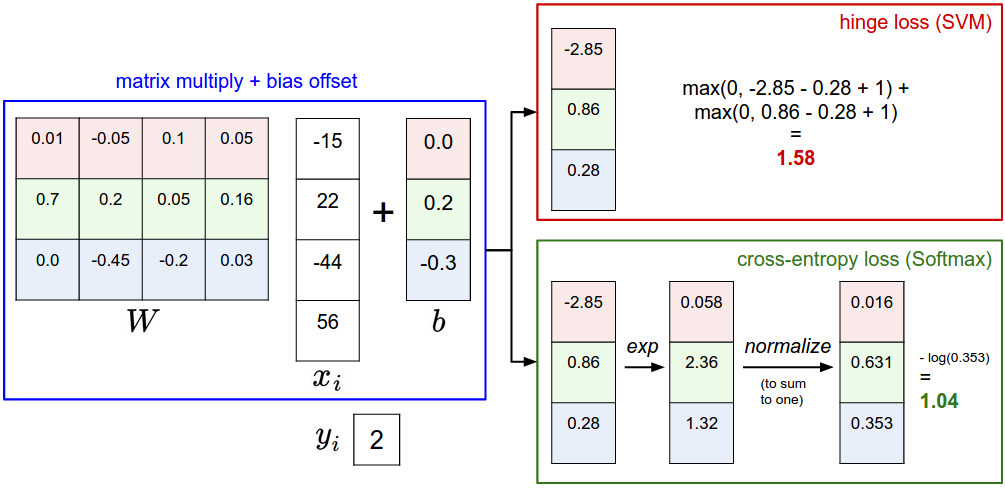
更精确一点。回想一下，对于第i个样本，给定图片\(x_i\)和标签\(y_i\)确定正确分类的索引。分数函数通过图片像素计算分类得分\(f(x_i,W)\)，我们简写作\(s\)。比如：第j个分类的得分就表示为第j个元素：\(s_j=f(x_i,W)_j\)。第i个样本的多类SVM损失可公式化表示如下：
$$L_i=\sum_{j≠y_i}{max(0,s_j-s_{y_i}+Δ)}$$

例子 下面以一个例子来说明它是如何工作的。假定有三个分类及其得分\(s=[13,-7,11]\)，并且第一个分类是正确的分类(\(y_i=0\),\(y_i\):分类索引值)。另外假定Δ(超参数，接下来将讲到)为10。上述公式是对所有不正确的分类求和(\(j≠y_i\))，所以得到：
$$L_i=max(0,-7-13+10)+max(0,11-13+10)$$
很显然max(0,-7-13+10)结果为0，这是因为正确分类得分(13)高于错误分类得分至少10(固定Δ值)分。实际上是20分，远大于10分，但是SVM只关注两者差异至少是10分(差异高于10分的一律设置为0)。max(0,11-13+10)结果为8。也就是说，即使正确分类得分比不正确分类得分高(13>11)，但差异不超过固定余量10。实际上差异是2，所以损失结果输出为8(为满足余量值所需的差异值大小)。总的来说，SVM损失函数期望正确分类得分\(y_i\)高于不正确分类得分至少Δ。如果不是，就需要累积损失。
注意到我们用的这个模块用了线性得分函数(\(f(x_i;W)=Wx_i\))，所以我们可以将损失函数等效为：
$$L_i=\sum_{j≠y_i}max(0,w_j^Tx_i-w_{y_j}^Tx_i+Δ)$$
其中，\(w_j\)是\(W\)的第j行转置成列。但是如果我们用更复杂的得分函数，情况就不一定了。
上述max(0,-)函数经常被称作hinge loss。有时会听到人们会用平方hinge loss SVM(L2-SVM)来代替，对应于\(max(0,-)^2\)，这会加强对偏离余量值的‘惩罚’。未平方版本更标准，但在某些数据集上，平方hinge loss会表现更好，这取决于交叉验证阶段的操作。

损失函数量化了对训练集预测结果的不满

正则化 上面提出的损失函数存在一个bug。假定我们有一个数据集和一个满足所有样本的参数集\(W\)(即所有得分满足上述规则，\(L_i=0\))。问题是\(W\)集可能不是唯一的：可能存在许多\(W\)的相似集满足样本。有一个简单方法验证：如果参数集\(W\)满足所有样本，那么参数集\(λW\)(λ>1)也将给出0损失，因为这个操作是对所有参数的统一拉伸，因它们的绝对差值也是如此。比如，如果正确分类得分和临近不正确分类得分差值是15，对所有\(W\)中元素乘2将会得到新的差值30。
换句话讲，我们希望对权重集\(W\)进行某种程度上的编码来消除这种歧义性。我们可以用regularization penalty R(W)(正则化惩罚)来扩展损失函数。最常用的正则化惩罚是L2范数，它通过对所有参数的元素二次惩罚来阻止大权重：$$R(W)=\sum_{k}\sum_{l}W_{k,l}^2$$
上面表达式，我们对\(W\)的元素平方求和。注意到正则化函数不是与数据(图像)的函数——它仅仅是基于权重的函数。正则化惩罚完善了多类SVM，包含两部分：数据损失(所有样本数据的平均损失\(L_i\))、正则化损失。也即，完整的多类SVM表示如下：
$$L = \underbrace{ \frac{1}{N} \sum_i L_i }\text{data loss} + \underbrace{ \lambda R(W) }\text{regularization loss} $$
或者以完整形式扩展：
\(L = \frac{1}{N} \sum_i \sum_{j\neq y_i} \left[ \max(0, f(x_i; W)_j - f(x_i; W)_{y_i} + \Delta) \right] + \lambda \sum_k\sum_l W_{k,l}^2\)
其中，N是训练样本的数量。将正则化惩罚加上去，用超参量λ作为权重。这个超参量通常取决于交叉验证。
除了上述提到的原因之外，正则化惩罚还有许多理想的属性，我们将会在随后讲到。例如，事实证明，加入L2惩罚会使得SVM中具有更吸引力的最大边缘属性。(CS229中将会详细讲到)
最吸引人的特性是惩罚大权重会改善(分类器)泛化性能，因为这意味着输入维度对最终得分没有影响。例如，假定我们有输入向量：\(x=[1,1,1,1]\)和两个权重向量：\(w_1=[1,0,0,0]\),\(w_2=[0.25,0.25,0.25,0.25]\)。那么\(w_1^Tx=w_2^Tx=1\)，两个权重向量会产生相等的点积，但是对\(w_1\)的L2惩罚是1.0而对\(w_2\)的L2惩罚仅为0.25。所以，根据L2惩罚，权重向量\(w_2\)表现更好因为它实现了跟你更低的正则化损失。直观上是因为权重\(w_2\)更小且更弥散。L2惩罚更偏向于小且弥散的权重向量，’the final classifier is encouraged to take into account all input dimensions to small amounts rather than a few input dimensions and very strongly’。后面我们将看到，这个影响能够改善分类器在测试集上的泛化性能并拥有较低的过拟合。
注意到偏差不像权重值那样的影响强度。因此通常知识调整权重而不是偏差。然而，在实际操作中，这经常会产生一些细微的影响。最后，注意到因为正则化惩罚，我们无法在所有样例中实现0.0的精确损失。
代码 这里给出了损失函数(未正则化)的Python实现(未矢量和半矢量形式)：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

def L_i(x, y, W):
  """
  unvectorized version. Compute the multiclass svm loss for a single example (x,y)
  - x is a column vector representing an image (e.g. 3073 x 1 in CIFAR-10)
    with an appended bias dimension in the 3073-rd position (i.e. bias trick)
  - y is an integer giving index of correct class (e.g. between 0 and 9 in CIFAR-10)
  - W is the weight matrix (e.g. 10 x 3073 in CIFAR-10)
  """
  delta = 1.0 # see notes about delta later in this section
  scores = W.dot(x) # scores becomes of size 10 x 1, the scores for each class
  correct_class_score = scores[y]
  D = W.shape[0] # number of classes, e.g. 10
  loss_i = 0.0
  for j in xrange(D): # iterate over all wrong classes
    if j == y:
      # skip for the true class to only loop over incorrect classes
      continue
    # accumulate loss for the i-th example
    loss_i += max(0, scores[j] - correct_class_score + delta)
  return loss_i

def L_i_vectorized(x, y, W):
  """
  A faster half-vectorized implementation. half-vectorized
  refers to the fact that for a single example the implementation contains
  no for loops, but there is still one loop over the examples (outside this function)
  """
  delta = 1.0
  scores = W.dot(x)
  # compute the margins for all classes in one vector operation
  margins = np.maximum(0, scores - scores[y] + delta)
  # on y-th position scores[y] - scores[y] canceled and gave delta. We want
  # to ignore the y-th position and only consider margin on max wrong class
  margins[y] = 0
  loss_i = np.sum(margins)
  return loss_i

def L(X, y, W):
  """
  fully-vectorized implementation :
  - X holds all the training examples as columns (e.g. 3073 x 50,000 in CIFAR-10)
  - y is array of integers specifying correct class (e.g. 50,000-D array)
  - W are weights (e.g. 10 x 3073)
  """
  # evaluate loss over all examples in X without using any for loops
  # left as exercise to reader in the assignment

本节的内容是SVM损失采用一种特定的方法来测量训练数据的预测与真值标签的一致性。 此外，对训练集进行良好预测相当于最大限度地减少损失。

我们需要做的就是提出一种找到满足最小损失的方法

实际考虑因素

设置Δ 应该设为什么？需不需要进行交叉验证？实际上，超参量Δ在所有例子中可以被安全地设置为1.权重\(W\)的大小直接影响到最后的得分(和他们的差异)：因为我们缩小了\(W\)的值，得分之间的差异将会更低，另一方面我们放大了权重值，这会使得分之间的差异变大。因此，得分边界的确切值(e.g. Δ=1 or Δ=100)是没有意义的，因为权重可以随意缩放差异值。因此，唯一的权衡是允许权重值增长程度(通过正则化强度λ)。
和二进制支持向量机的关系 二进制支持向量机下第i个样例的损失表示如下：$$L_i=Cmax(0,1-y_iw^Tx_i)+R(W)$$其中\(C\)是超参量，\(y_i \in {-1,1}\)。可以把二进制支持向量机理解为我们之前提出的多类SVM的一种特例：如果只有两个分类，多类SVM就成了二进制SVM。上述公式中的\(C\)和我们之前公式中的\(λ\)控制着相同的权衡，并且是倒数关系\(C \propto \frac{1}{\lambda}\)。
原始优化 如果你以前了解SVM知识，你可能听说过内核，双重，SMO算法等。在这个课程中（神经网络）我们将一直使用无约束原始形式的优化目标。这些目标中的许多在技术上是不可微分的(例如，max(x，y)函数，因为当x=y时它具有扭结)，但实际上这不是问题，并且通常使用子梯度。
其他多类SVM公式化 值得注意的是，本节提出的多类SVM是多个多类SVM公式化中的一个。另一个常用的公式是One-Vs-All(OVA)SVM，它为每个分类单独训练二进制SVM。还有不太常用的All-vs-All(AVA)策略。我们的公式遵从Weston and Watkins 1999 (pdf) 版本，这是一个比OVA更强大的版本(从某种意义上说，你可以构建多版本数据集，其中这个版本可以实现零数据损失，但OVA不能。如果感兴趣，请参阅论文)。最后是结构化SVM，它可以最大化正确分类得分与得分次高间的差距。理解这些公式之间的差异超出本课程范围。本节提出的版本是实际操作安全的，但最简单的OVA策略也可能同样有效

　Softmax分类器

SVM是两个常用的分类器之一，另一个是Softmax classifier。如果你之前听过二进制Logistic Regression分类器，Softmax分类器是它在多类上的推广。不同于SVM将输出\(f(x_i,W)\)作为每个分类的得分，Softmax分类器给出一个更直观的输出(标准化类概率)，和稍后将讲到的概率解释。在Softmax分类器中，函数映射\(f(x_i;W)=Wx_i\)不变，但我们现在将这些分类得分解释为每个分类的非标准化对数概率，并用具有以下形式的交叉熵损失替换hinge损失：$$L_i = -\log\left(\frac{e^{f_{y_i}}}{ \sum_j e^{f_j} }\right) \hspace{0.5in} \text{or equivalently} \hspace{0.5in} L_i = -f_{y_i} + \log\sum_j e^{f_j}$$用\(f_j\)表示分类得分向量\(f\)的第j个元素。像之前一样，数据集的全部损失是所有训练样例\(L_i\)的平均值，有一个正则化术语\(R(W)\)。函数\(f_j(z) = \frac{e^{z_j}}{\sum_k e^{z_k}}\)被称作softmax function:它将任意真值得分向量压缩到值为0到1之间且和为1的向量。如果是第一次接触，softmax函数中涉及到的全交叉熵损失看起来很可怕，实际上相对容易激励。
信息论观点 “真实”分布\(p\)和预测分布\(q\)之间的交叉熵定义为：$$H(p,q) = - \sum_x p(x) \log q(x)$$Softmax分类器最小化两者之间的交叉熵(\(q = e^{f_{y_i}} / \sum_j e^{f_j}\))，which in this interpretation is the distribution where all probability mass is on the correct class (i.e. \(p=[0,…1,…,0]\)contains a single 1 at the\(y_i\)-th position.)。此外，因为交叉熵可以被写作\(H(p,q) = H(p) + D_{KL}(p||q)\)，Δ函数\(p\)的熵为0，等同于两个分布之间KL差异(一种距离测量)的最小化。换句话说，交叉熵客观上_希望_预测分布能够在正确答案上有全部的质量。
概率解释 下式：$$P(y_i \mid x_i; W) = \frac{e^{f_{y_i}}}{\sum_j e^{f_j} }$$可以解释为给定图像\(x_i\)和参数化\(W\)的正确标签\(y_i\)分配的（标准化）概率？？？Softmax分类器将输出向量\(f\)中的得分解释为未标准化的对数概率。指数化这些量给出的概率，并且执行除法归一化，使概率和为1。在这个概率解释中，我们因此最小化正确分类的负对数似然(这可以被解释为执行最大似然估计，MLE)。这种观点有个良好的特性，使得我们能够解释来自高斯先验超权重矩阵的完全损失函数中的正则化项\(R(W)\)，而不是我们正在执行的最大后验(MAP)估计。我们提到这些解释来帮助你的直觉，但推导的细节超出本课程范围。
实际问题：数字稳定性 在实际编写用于计算Softmax函数的代码时，中间项\(e^{f_{y_i}}\)和\(\sum_j e^{f_j}\)会由于指数(运算)而变得非常大。划分大数值可能不稳定，因此使用归一化技巧很重要。请注意：如果我们将分子分母同乘一个常量C，并分别相加，我们得到下述表达式：\(\frac{e^{f_{y_i}}}{\sum_j e^{f_j}}= \frac{Ce^{f_{y_i}}}{C\sum_j e^{f_j}} = \frac{e^{f_{y_i} + \log C}}{\sum_j e^{f_j + \log C}}\) \(C\)的值可以自由选择，这不会对结果造成影响，我们可以借助这个值来改善计算数值的稳定性。常用的选择是将其设为\(logC=-max_jf_j\)。代码实现如下：

1
2
3
4
5
6

f = np.array([123, 456, 789]) #假设有3个分类获得较大的得分
p = np.exp(f) / np.sum(np.exp(f)) #坏:数值计算问题，潜在爆炸性计算

#改善:左移f值，使得最大数字为0:
f -= np.max(f) #f变为[-666, -333, 0]
p = np.exp(f) / np.sum(np.exp(f)) # 安全计算，给出正确值

命名约定 确切来讲，SVM分类器使用hinge loss，或者有时候称作max-margin(最大边界) loss。Softmax分类器使用cross-entropy(交叉熵) loss。Softmax分类器名字来源于softmax函数，该函数用于将原始类分数压缩为归一化的正值，以便可以应用交叉熵损失。在实际中，需要注意的是：技术上谈论softmax损失是没有意义的，因为softmax只有压缩作用，但是它是一种相当常用的简写。

　SVM vs. Softmax

Softmax分类器提供了每个分类的可能性 与计算所有类别的未校准且不易解释的SVM不同，Softmax分类器允许我们计算所有分类的“概率”。例如：给定一个图片，SVM分类器可能给出标签为“猫，狗，船”的得分[12.5,0.6,-23.0]。Softmax分类器则将计算这三个分类的概率为[0.9,0.09,0.01]。然而，我们将概率加引号是因为这些概率的峰值或者扩散程度如何将直接取决于正则化强度\(λ\)-您负责作为系统的输入。例如：假定三个分类的非标准化对数概率输出为[1,-2,0]。Softmax函数计算如下：
$$[1, -2, 0] \rightarrow [e^1, e^{-2}, e^0] = [2.71, 0.14, 1] \rightarrow [0.7, 0.04, 0.26]$$
这一步是做了指数化和归一化。如果正则强度\(λ\)太高，权重\(W\)将会做更多惩罚以此来获得更小的权重。例如，假定权重变为原来一半([0.5,-1,0])，Softmax计算如下：
$$[0.5, -1, 0] \rightarrow [e^{0.5}, e^{-1}, e^0] = [1.65, 0.37, 1] \rightarrow [0.55, 0.12, 0.33]$$
现在概率更加分散。此外，由于非常强的正则化强度λ，权重朝向微小数量的极限，输出概率几乎是均匀的。因此，由Softmax分类器计算的概率更好地被认为是置信度，其中类似于SVM，分数的排序是可解释的，但绝对数字（或它们的差异）在技术上不是。

实际上，SVM和Softmax通常具有可比性 SVM和Softmax之间的性能差异通常很小，并且，不同的人对哪种分类器更好持有不同的观点。和Softmax分类器相比，SVM更local objective，这可以被当作是bug或者特性。考虑这样一个例子：分类得分为[10,-2,3]并且第一个分类是正确的分类。SVM(eg. \(Δ=1\))认为正确分类得分和其他分类得分差距已经超过边界值，因此计算的损失值为0。SVM不关心单个得分的细节：如果得分为[10,-100,-100]或者[10,9,9]，尽管边界值1是满足的，但是SVM是无关紧要的，因此损失值是0。然而对于Softmax分类器，情况是不一样的，得分[10,9,9]相比于[10,-100,-100]会积累更多的损失值。换句话说，Softmax分类器从不完全满意它产生的分数：正确的类总是有更高的概率，不正确的类总是更低的概率，并且损失总是会变得更好。然而SVM是一旦边际得到满足就会满意，并且它不会对超出次约束的精确得分进行微观管理。这可以直观地理解为一个特性：例如，一个汽车分类器可能将大部分“努力”用于将汽车从卡车上分离出来，不应受到青蛙分类(已经被分配非常低的得分并且可能聚集在数据云的完全不同的一侧)的影响

　Interactive web demo

演示地址：http://vision.stanford.edu/teaching/cs231n-demos/linear-classify/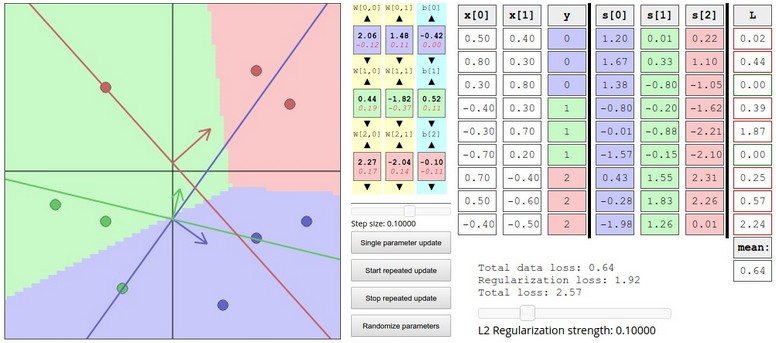

总结

总结：

定义从图像像素到分类得分的得分函数(本节中是依赖于权重W和偏差b的线性函数)
不同于kNN分类器，这种参数法的优势在于一旦我们学习到这些参数值，就可以抛弃训练数据。除此之外，对测试图片的预测会很快因为它只需要一次矩阵乘法而不是去和每个训练样本比较
引入偏差技巧，允许我们将偏差向量合并到权重矩阵中
定义损失函数(我们为线性分类器引入了两个通用的损失函数：SVM和Softmax)来衡量训练集中给定参数和真值标签之间的兼容性。我们还发现这种方式定义的损失函数是对训练数据做出良好的预测相当于损失很小。

我们现在看到了一种方法来获取图像数据集，并根据一组参数将每个图像映射到类别得分，我们看到了两个可用于衡量预测质量的损失函数示例。但是，我们如何有效地确定产生最佳（最低）损失的参数？这个过程是优化，它是下一节的主题。