CS231n用于视觉识别的卷积神经网络-学习笔记3-优化：随机梯度下降

原文地址：http://cs231n.github.io/optimization-1/
翻译：Archiew 　转载需注明出处

线性分类

目录
引入
可视化损失函数
优化
　策略 #1:随机搜索
　策略 #2:随机局部搜索
　策略 #3:跟随梯度
梯度计算
　有限差分数值计算梯度
　微积分分析
梯度下降
总结

---

引入

前两讲中我们介绍了图片分类问题的两个关键任务：

1. 从图片像素到分类得分的映射：(参数化)得分函数(e.g. 线性函数)
2. 衡量训练数据诱导得分和分类真值一致性质量的损失函数，我们了解到有很多方法和版本9)
   具体讲，回想线性函数公式\(f(x_i,W)=Wx_i\)和SVM公式$$L = \frac{1}{N} \sum_i \sum_{j\neq y_i} \left[ \max(0, f(x_i; W)_j - f(x_i; W)_{y_i} + 1) \right] + \alpha R(W)$$我们看到参数\(W\)的设置对样例\(x_i\)的预测与它们真值标签\(y_i\)相一致，这将会产生低的损失值\(L\)。接下来我们将要介绍最后一个关键部分：优化。优化指的是找出一组参数\(W\)使损失函数最小化。
   伏笔 一旦我们理解了这三个核心部分如何相互作用，我们将回到第一部分(参数化函数映射)将其扩展为一个比线性映射更加复杂的函数：首先是全神经网络，其次是卷积神经网络。损失函数和优化过程将保持相对不变。

可视化损失函数

本节中我们将会看到损失函数通常被定义为高维空间(e.g. 在CIFAR-10中，线性分类器权重矩阵大小为[10X3073]，共30730个参数)，这使得它们难以可视化。但是，我们仍可以通过沿着光线(1维)或平面(2维)切割高维空间来获得某种程度的直观。比如，我们可以产生一个随机权重矩阵\(W\)(对应于空间中的单个点)，然后沿光线行进并记录损失函数值。也就是说，我们可以产生一个随机方向\(W_1\)并通过求不同\(a\)对应的\(L(W+aW_1)\)的值来计算该方向上的损失(值)。该过程产生一个简单的图，该图以\(a\)的值为x轴以损失函数值为y轴。我们也可以通过计算以\(a\)和\(b\)为变量的损失\(L(W+aW_1+bW_2)\)的值来获得二维图，在图中，\(a\)和\(b\)对应于x轴和y轴，损失函数值可被可视化为颜色。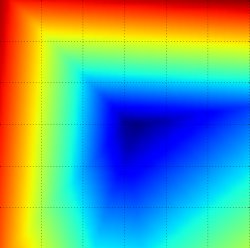

上述损失函数的分段线性结构可以通过数学公式来解释。对单一样例，我们有：$$L_i = \sum_{j\neq y_i} \left[ \max(0, w_j^Tx_i - w_{y_i}^Tx_i + 1) \right]$$表达式明显地表明每个样例的损失数据是线性函数\(W\)的求和。此外，有时候\(W\)的每行(i.e. \(w_j\))在它前面都有一个正号(对应于一个例子的错误类)，有时候是负号(对应于该样例的正确类)。为使其更明确，考虑一个简单的包含三个一维点和三个分类的数据集。全SVM损失(未正则化)变成：
$$
L_0 = \max(0, w_1^Tx_0 - w_0^Tx_0 + 1) + \max(0, w_2^Tx_0 - w_0^Tx_0 + 1) \\
L_1 = \max(0, w_0^Tx_1 - w_1^Tx_1 + 1) + \max(0, w_2^Tx_1 - w_1^Tx_1 + 1) \\
L_2 = \max(0, w_0^Tx_2 - w_2^Tx_2 + 1) + \max(0, w_1^Tx_2 - w_2^Tx_2 + 1) \\
L = (L_0 + L_1 + L_2)/3
$$
因为样例是一维的，数据\(x_i\)和权重\(w_j\)是数值。上述术语是\(w_0\)的线性函数，并且都被钳制在0。我们可以可视化如下：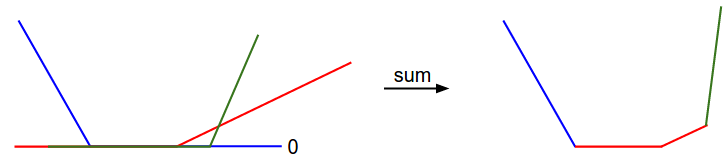

顺便说一句，你可能已经从它的碗状外观猜到了，SVM成本函数是凸函数的一个例子。有大量的文献致力于研究最小化这种类型的函数，您也可以参加斯坦福关于此话题的课程(凸优化)。一旦我们扩展得分函数\(f\)到神经网络，我们目标函数将会变为非凸的，并且上面的可视化不会呈现碗状特征，而是蜿蜒复杂的形状。

不可微分的损失函数。作为技术说明，你还可以在损失函数中看到kinks(转折点，因为最大化操作)，因为kinks处梯度未定义，所以使得损失函数不可微分。然而，子梯度依旧存在并且通常用于取代它。本节将会交替使用术语子梯度和梯度

优化

重申一下，损失函数可以让我们量化任何特定权重集\(W\)的质量。优化的目标是找到最小化损失函数的\(W\)。我们现在要开发一种方法优化损失函数。对之前有经验的同学，本节课可能看起来很奇怪因为我们将使用的样例(SVM损失)是一个凸问题，但是请记住我们的目的是最终优化不能轻易使用凸优化文献中开发的任何工具的神经网络。

　策略 #1:一个很糟糕的解决方案:随机搜索

由于检查给定参数集\(W\)的好坏是如此简单，因此可能想到的第一个(非常糟糕的)想法是简单地尝试许多不同的随机权重值并跟踪最佳效果，此过程看起来像下面这样：

# assume X_train is the data where each column is an example (e.g. 3073 x 50,000)
# assume Y_train are the labels (e.g. 1D array of 50,000)
# assume the function L evaluates the loss function

bestloss = float("inf") # Python assigns the highest possible float value
for num in xrange(1000):
  W = np.random.randn(10, 3073) * 0.0001 # generate random parameters
  loss = L(X_train, Y_train, W) # get the loss over the entire training set
  if loss < bestloss: # keep track of the best solution
    bestloss = loss
    bestW = W
  print 'in attempt %d the loss was %f, best %f' % (num, loss, bestloss)

# prints:
# in attempt 0 the loss was 9.401632, best 9.401632
# in attempt 1 the loss was 8.959668, best 8.959668
# in attempt 2 the loss was 9.044034, best 8.959668
# in attempt 3 the loss was 9.278948, best 8.959668
# in attempt 4 the loss was 8.857370, best 8.857370
# in attempt 5 the loss was 8.943151, best 8.857370
# in attempt 6 the loss was 8.605604, best 8.605604
# ... (trunctated: continues for 1000 lines)

上面的代码中，我们尝试了一些随机权重向量\(W\)，并且其中一些效果要优于其他的。我们可以通过这种搜索来找到最佳的权重\(W\)并且在测试集上尝试一下：

# Assume X_test is [3073 x 10000], Y_test [10000 x 1]
scores = Wbest.dot(Xte_cols) # 10 x 10000, the class scores for all test examples
# find the index with max score in each column (the predicted class)
Yte_predict = np.argmax(scores, axis = 0)
# and calculate accuracy (fraction of predictions that are correct)
np.mean(Yte_predict == Yte)
# returns 0.1555

利用最佳\(W\)，给出了大约15.5%的准确度。考虑到完全随机猜测有10%的准确度，对一个“脑死亡”随机搜索方法来讲，这不是最糟糕的！

核心理念：迭代求精 当然了，事实证明，我们可以做的更好核心理念是找到一组最佳的权重\(W\)是很困难的或者说是不可能的问题(特别是当\(W\)包含了整个复杂神经网络的权重)，但是将一组特定权重\(W\)精炼的更好的问题是不太困难的。换句话说，我们的方法是从一组随机\(W\)开始，然后迭代细化，使其每次都稍微好一点。

我们的策略是从一组随机权重\(W\)开始，然后在整个过程中迭代细化来找到最小损失。

Blindfolded hiker analogy 一个形象的比喻就是，想象自己带着眼罩在小山上徒步并试图达到底部。在CIFAR-10的例子中，因为\(W\)是10x3073，所以“小山”是30730维的。“小山”上的每一点我们都实现了特定损失(地形高度)。

　策略 #2:随机局部搜索

第一种策略是沿一个随机方向扩展，具体讲，我们以一个随机\(W\)开始，产生随机扰动\(δW\)，如果扰动处损失更低，我们就更新一次。此过程编码如下：

W = np.random.randn(10, 3073) * 0.001 # generate random starting W
bestloss = float("inf")
for i in xrange(1000):
  step_size = 0.0001
  Wtry = W + np.random.randn(10, 3073) * step_size
  loss = L(Xtr_cols, Ytr, Wtry)
  if loss < bestloss:
    W = Wtry
    bestloss = loss
  print 'iter %d loss is %f' % (i, bestloss)

使用和之前相同数量(1000)的损失函数评估，该方法实现了测试集上21.4%的预测分类准确度。有所改善，单仍耗费大量资源。

　策略 #3:跟随梯度

在先前讲解中，我们尝试在权重空间寻找一个方向来改善我们的权重向量(得到低损失值)。事实表明，我们没有必要随机搜索一个好的方向：我们可以计算出我们应该改变我们的权重向量的最佳方向，这在数学上保证是最陡下降的方向（至少在极限时为步长变为零）。该方向将与损失函数的梯度相关。在我们的徒步比喻中，这种方法大致相当于感知脚下山坡倾斜并沿着感觉最陡的方向走下去。
在一维函数中，斜率是函数在您感兴趣点处的瞬时变化率。梯度不是数值而是采用数值向量的函数的斜率的推广。除此之外，梯度是输入空间中每一维斜率矢量(通常称为导数)。关于其输入的一维函数导数表达式如下：
$$\frac{df(x)}{dx} = \lim_{h\ \to 0} \frac{f(x + h) - f(x)}{h}$$
当感兴趣的函数采用数值矢量而不是数值表示时，我们将导数称为偏导数，梯度只是每一维的偏导数的矢量。

梯度计算

有两种方法来计算梯度：一种是缓慢近似但简单的数值梯度，另一种时快速精确但更容易出错的解析梯度。下面我们将分别介绍两者。

　有限差分数值计算梯度

上面的公式允许我们计算数值梯度。这是一个泛型函数，输入函数f，矢量x来评估梯度，并返回函数f在x处的梯度：

def eval_numerical_gradient(f, x):
  """ 
  a naive implementation of numerical gradient of f at x 
  - f should be a function that takes a single argument
  - x is the point (numpy array) to evaluate the gradient at
  """ 

  fx = f(x) # evaluate function value at original point
  grad = np.zeros(x.shape)
  h = 0.00001

  # iterate over all indexes in x
  it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
  while not it.finished:

    # evaluate function at x+h
    ix = it.multi_index
    old_value = x[ix]
    x[ix] = old_value + h # increment by h
    fxh = f(x) # evalute f(x + h)
    x[ix] = old_value # restore to previous value (very important!)

    # compute the partial derivative
    grad[ix] = (fxh - fx) / h # the slope
    it.iternext() # step to next dimension

  return grad

按照上面给出的梯度公式，上面代码逐个迭代所有维度，h沿着改为度进行微小改变并通过查看函数值改变多少来计算损失函数沿该维度的偏导数，最后变量grad记录了完整的梯度。

实际考虑 注意，在数学上，梯度定义为当h趋近于于0时的极限，但是实际操作中使用非常小的值(示例中是0.00001)就够了。理想地，我们希望使用不会导致数值问题的最小步长。此外在实际中，使用居中差异公式\([f(x+h)-f(x-h)]/2h\)计算梯度通常会更好。详情请见wiki

利用上述公式我们可以计算任何函数任意点处的梯度。接下来我们计算CIFAR-10中损失函数在权重空间随机点处的梯度：

# to use the generic code above we want a function that takes a single argument
# (the weights in our case) so we close over X_train and Y_train
def CIFAR10_loss_fun(W):
  return L(X_train, Y_train, W)

W = np.random.rand(10, 3073) * 0.001 # random weight vector
df = eval_numerical_gradient(CIFAR10_loss_fun, W) # get the gradient

梯度表明了每一维损失函数的斜率，我们可以以此来更新:

loss_original = CIFAR10_loss_fun(W) # the original loss
print 'original loss: %f' % (loss_original, )

# lets see the effect of multiple step sizes
for step_size_log in [-10, -9, -8, -7, -6, -5,-4,-3,-2,-1]:
  step_size = 10 ** step_size_log
  W_new = W - step_size * df # new position in the weight space
  loss_new = CIFAR10_loss_fun(W_new)
  print 'for step size %f new loss: %f' % (step_size, loss_new)

# prints:
# original loss: 2.200718
# for step size 1.000000e-10 new loss: 2.200652
# for step size 1.000000e-09 new loss: 2.200057
# for step size 1.000000e-08 new loss: 2.194116
# for step size 1.000000e-07 new loss: 2.135493
# for step size 1.000000e-06 new loss: 1.647802
# for step size 1.000000e-05 new loss: 2.844355
# for step size 1.000000e-04 new loss: 25.558142
# for step size 1.000000e-03 new loss: 254.086573
# for step size 1.000000e-02 new loss: 2539.370888
# for step size 1.000000e-01 new loss: 25392.214036

以负梯度方向更新 上面的代码中注意到为了计算W_new，我们在梯度df的负方向上进行更新，因为我们希望损失函数减少而不是增加。

步长影响 梯度告诉我们函数最陡增长率的方向，但并没有告诉我们应该沿该方向走多远。我们将在后续课程中看到，步长(也叫学习率)的选择将成为训练神经网络超参设置中最重要(最头疼)的一部分。在我们的“遮眼下山”比喻中，我们感知脚下山坡向某个方向倾斜，但步长是不确定的。如果我们小心地移动